2016-06-25

楽しい圏論(その 4)

今後, ${F(a), F(f)}$ などは単に ${Fa, Ff}$ と書きます. また, 射や函手の合成記号は省いて ${gf, GF}$ などと書きます.

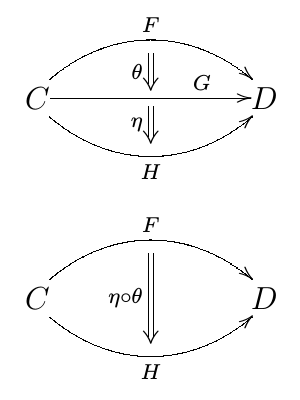
自然変換の垂直合成と函手圏

圏 ${C}$ から圏 ${D}$ への函手 ${F, G, H : C \to D}$ と自然変換 ${\theta : F \Rightarrow G, \eta : G \Rightarrow H}$ が与えられたとき, 垂直合成(vertical composition) ${\eta \circ \theta}$ を ${(\eta \circ \theta)_a := \eta_a \theta_a \ (a \in \mathcal{O}(C))}$ で定義します.

これが ${F}$ から ${H}$ への自然変換になっていることは, 次図の可換性から明らかでしょう.

${\require{AMScd}\begin{CD} Fa @>{Ff}>> Fb \\ @V{\theta_a}VV @VV{\theta_b}V \\ Ga @>{Gf}>> Gb \\ @V{\eta_a}VV @VV{\eta_b}V \\ Ha @>>{Hf}> Hb, \end{CD}}$
${(a, b \in \mathcal{O}(C), f \in C(a,b).)}$

自然変換の垂直合成は結合法則を満たし, これによって ${C}$ から ${D}$ への函手の全体は函手を対象, 自然変換を射とする圏になります. これを函手圏(functor category)と言い, ${D^C}$ で表します.

自然変換の水平合成

自然変換にはもう一つ, 水平合成(horizontal composition)と言われる合成があります. これは次図のように圏 ${C}$ から圏 ${D}$ への函手 ${F_0, F_1 : C \to D}$ と, 圏 ${D}$ から圏 ${E}$ への函手 ${G_0, G_1 : D \to E}$ , さらに自然変換 ${\theta : F_0 \Rightarrow F_1, \eta : G_0 \Rightarrow G_1}$ があるときに定義されます.

以下, 長くなるので折りたたみ.

2016-06-19

楽しい圏論(その 3)

数学・基礎論

反変函手と双対圏

前回は函手を定義しましたが, もう一つ, 反変函手(contravariant functor)と言われるものがあります.

${e}$ が ${\mathcal{M}_1}$ の恒等射ならば ${F(e)}$ は ${\mathcal{M}_2}$ の恒等射である.
${\mathcal{M}_1}$ において ${xy}$ が定義されているならば ${\mathcal{M}_2}$ において ${F(y)F(x)}$ が定義されており, ${F(xy) = F(y)F(x)}$ である.

一つ目は通常の函手(共変函手(covariant functor)と言われることもあります)と同じですが, 二つ目が変わっていて, 反変函手の場合は射の合成の順番が入れ替わります.

反変函手は, 以下のような双対圏(dual category)の概念を導入することで, 共変函手と区別することなく扱うことができます.

${\mathcal{M}}$ を射のクラスとするとき, 双対射のクラス ${\mathcal{M}^{\mathrm{op}} = \{x^{\mathrm{op}} | x \in \mathcal{M}\}}$ において ${x^{\mathrm{op}} y^{\mathrm{op}} = (yx)^{\mathrm{op}}}$ と定めます. ${e \in \mathcal{M}}$ が恒等射ならば ${e^{\mathrm{op}} \in \mathcal{M}^{\mathrm{op}}}$ も恒等射です. ${(1_A)^{\mathrm{op}} = 1_{A^{\mathrm{op}}}}$ となるように定めることで ${\mathcal{O}^{\mathrm{op}} = \{A^{\mathrm{op}} | A \in \mathcal{O}\}}$ と表せます.

このとき

${D(x)^{\mathrm{op}}}$ は恒等射
${D(x)^{\mathrm{op}} x^{\mathrm{op}} = (xD(x))^{\mathrm{op}}}$ は定義されている

ので, ${R(x^{\mathrm{op}}) = D(x)^{\mathrm{op}}}$ です. 同様に ${D(x^{\mathrm{op}}) = R(x)^{\mathrm{op}}}$ です. よって ${A \overset{x}{\longrightarrow} B}$ は双対圏において ${B^{\mathrm{op}} \overset{x^{\mathrm{op}}}{\longrightarrow} A^{\mathrm{op}}}$ に変換されます.

${A \in \mathcal{O}}$ と ${A^{\mathrm{op}} \in \mathcal{O}^{\mathrm{op}}}$ を同一視することによって, 双対圏とは射の向きを逆にしたもの, と考えることができます.

双対圏を使うと反変函手 ${F : \mathcal{M}_1 \to \mathcal{M}_2}$ は共変函手 ${F : {\mathcal{M}_1}^{\mathrm{op}} \to \mathcal{M}_2}$ とみなせるため, 以下は反変函手もこの同一視によって単に「函手」と言うことにします.

自然変換

最後に自然変換を定義します.

二つの函手 ${F, G : \mathcal{C}_1 \to \mathcal{C}_2}$ があるとき, ${\eta : F \Rightarrow G}$ が自然変換(natural transformation)であるとは, 以下の公理を満たすことを言います.

${A \in \mathcal{O}_1}$ に対して ${\eta(A) \in \mathcal{C}_2(F(A), G(A)).}$
${x \in \mathcal{C}_1(A, B)}$ に対して次図は可換である.

${\require{AMScd}\begin{CD} F(A) @>{F(x)}>> F(B) \\ @V{\eta(A)}VV @VV{\eta(B)}V \\ G(A) @>>{G(x)}> G(B) \end{CD}}$

(標数 ${0}$ の体 ${K}$ 上の)有限次元ベクトル空間 ${V}$ について ${V^* := \hom(V, K)}$ とするとき, 「自然な」同型 ${V \cong V^{**}}$ があるのですが, この自然な, という意味は以下の通りです.

${\theta_V : V \to V^{**}}$ を ${\theta_V(x)(\varphi) = \varphi(x) \ (x \in V, \varphi \in V^*)}$ で定めるとき, 任意の線形写像 ${f : V \to W}$ に対して ${f^{**} \circ \theta_V = \theta_W \circ f}$ が成り立ちます. ただし ${f^* : W^* \ni \psi \mapsto \psi \circ f \in V^*.}$ 実際, 任意の ${x \in V}$ と ${\psi \in W^*}$ に対して

${\begin{align} (f^{**} \circ \theta_V)(x)(\psi) &= (\theta_V(x) \circ f^*)(\psi) \\ &= \theta_V(x)(\psi \circ f) \\ &= \psi(f(x)), \end{align}}$
${\begin{align} (\theta_W \circ f)(x)(\psi) &= \theta_W(f(x))(\psi) \\ &= \psi(f(x)). \end{align}}$

従って次図は可換になります.

${\require{AMScd}\begin{CD} V @>{f}>> W \\ @V{\theta_V}VV @VV{\theta_W}V \\ V^{**} @>>{f^{**}}> W^{**} \end{CD}}$

以上の証明には ${V}$ が有限次元であることは使っていませんが, ${V}$ が有限次元ならば ${\theta_V : V \to V^{**}}$ は同型写像になります.

元々は, このような現象を一般化する概念として自然変換を定義するべく, 函手や圏の概念ができていったようです.

記法の約束事

今後の記法に関する約束事です.

圏 : アルファベット大文字 ${C, D, \dots}$
対象 : アルファベット小文字 ${a, b, \dots}$ , 圏 ${C}$ の対象の全体は ${\mathcal{O}(C)}$ で表す.
射 : アルファベット小文字 ${f, g, h, \dots}$ , 圏 ${C}$ の対象 ${a}$ から ${b}$ への射の全体は ${C(a, b)}$ で表す.
函手 : アルファベット大文字 ${F, G, H, \dots}$
自然変換 : ギリシャ小文字 ${\theta, \eta, \dots}$

2016-06-16

楽しい圏論(その 2)

数学・基礎論

一ヶ月ほど間が空いてしまいましたが, ようやくブログを書ける状態になってきたので再開します.

函手の定義

${\mathcal{M}_1, \mathcal{M}_2}$ を二つの圏(の射のクラス)とします. クラス関数 ${F : \mathcal{M}_1 \to \mathcal{M}_2}$ は, 以下の二つの公理を満たすとき, 函手(functor)であると言います.

${e}$ が ${\mathcal{M}_1}$ の恒等射ならば ${F(e)}$ は ${\mathcal{M}_2}$ の恒等射である.
${\mathcal{M}_1}$ において ${xy}$ が定義されているならば ${\mathcal{M}_2}$ において ${F(x)F(y)}$ が定義されており, ${F(xy) = F(x)F(y)}$ である.

${\mathcal{O}_1, \mathcal{O}_2}$ をそれぞれ ${\mathcal{M}_1, \mathcal{M}_2}$ に対応する対象のクラスとするとき, ${A \in \mathcal{O}_1}$ に対して ${F(A) \in \mathcal{O}_2}$ を
${1_{F(A)} = F(1_A)}$
なる対象と定めることにより, ${F}$ はクラス関数 ${F : \mathcal{O}_1 \to \mathcal{O}_2}$ を導きます.

前回, 射の値域と定義域の話をしました. ${1_B = R(x)}$ を満たす ${B}$ のことを ${Range(x)}$ と, また ${1_A = D(x)}$ を満たす ${A}$ のことを ${Domain(x)}$ と書くことにします.

命題 0.4. ${F(Domain(x)) = Domain(F(x)), F(Range(x)) = Range(F(x)).}$

(証明)*1

${F(D(x))}$ は恒等射で, かつ ${F(x)F(D(x)) = F(xD(x))}$ が定義されているから ${F(D(x)) = D(F(x)).}$ 同様に ${F(R(x)) = R(F(x)).}$ 以上から従う. ■

タネ本

何だか射の話ばかりが出てきて, 多分他の書籍で圏論を知った人は驚くかも知れませんが, これでちゃんと理論になっています. この方法にはタネ本があります.

Abelian Categories

作者: Peter Freyd
出版社/メーカー: Joanna Cotler Books
発売日: 1966/12
メディア: ハードカバー
この商品を含むブログを見る

(自分が持っているものとは出版社が違いますが, 中身は多分同じ ?)

この本では, 今回のようなやり方で圏と函手を定義しています.

特殊な圏

以下, 頻繁に(?)使用する特殊な圏をいくつか定義します.

射のクラスが空集合である圏を空圏と言い, ${\boldsymbol{0}}$ で表します. もちろん, 空圏には対象も存在しません.

射のクラスがただ一つの恒等射だけからなる圏を ${\boldsymbol{1}}$ で表します. ${\boldsymbol{1} = (\{*\}, \{1_*\}).}$

射のクラスが二つの恒等射 ${1_A, 1_B}$ と, 恒等射ではないただ一つの射 ${x \ (D(x) = 1_A, R(x) = 1_B)}$ の三つの元からなる集合である圏を ${\boldsymbol{2}}$ で表します. これは後で述べるように, 集合 ${\{0, 1\}}$ に通常の大小関係で定まる順序を入れた順序集合を圏とみなしたものと同じです.

射のクラスが

三つの恒等射 ${1_A, 1_B, 1_C}$
恒等射でない二つの射 ${x, y \ (D(y) = 1_A, R(y) = D(x) = 1_B, R(x) = 1_C)}$ とその合成 ${xy}$

の 6 個の元からなる集合である圏を ${\boldsymbol{3}}$ で表します. これも後で述べるように, 集合 ${\{0, 1, 2\}}$ に通常の大小関係で定まる順序を入れた順序集合を圏とみなしたものと同じです.

射のクラスが, 二つの恒等射 ${1_A, 1_B}$ と恒等射でない二つの射 ${x, y}$ からなり, ${D(x) = D(y) = 1_A}$ かつ ${R(x) = R(y) = 1_B}$ であるものとします. この圏は ${\downdownarrows}$ で表します.

順序集合は圏である

${A}$ が順序集合であるとは, 台集合 ${A}$ と関係 ${O \subset A \times A}$ の組 ${(A, O)}$ が以下の条件を満たすことでした.

(反射律) ${\Delta_A \subset O,}$ ただし ${\Delta_A = \{(a, a) | a \in A\}}$ は対角集合.
(反対称律) ${O \cap O^{-1} = \Delta_A,}$ ただし ${O^{-1} = \{(b, a) | (a, b) \in O\}}$ は逆関係.
(推移律) ${O \circ O \subset O,}$ ただし ${O \circ O = \{(a, c) | (\exists b \in A)((a, b) \in O \wedge (b, c) \in O)\}}$ は関係の合成.

そこで, ${O}$ を射の集合として, 射の合成を ${(b, c) \circ (a, b) = (a, c)}$ で定めると, これを圏とみなすことができます. ${1_a = (a, a)}$ なる対応によって, ${A}$ を対象の集合とみなすことができます.

このことを使うと, 通常の数の大小関係による順序付けでもって
${\boldsymbol{2} = \{0, 1\}, \boldsymbol{3} = \{0, 1, 2\}}$
となることがわかります.

対象は函手であり, 射は函手である.

圏 ${\mathcal{C}}$ の対象は函手 ${A : \boldsymbol{1} \to \mathcal{C}}$ とみなすことができます. また ${\mathcal{C}}$ の射は函手 ${x : \boldsymbol{2} \to \mathcal{C}}$ とみなすことができます.

*1:タネ本では「特に証明することはない」と書いていますが, ざっくりと説明しておきます.

2016-05-17

楽しい圏論(その 1)

数学・基礎論

今回から, 圏論について述べていこうと思います. Heyting 代数の話の中でも, 一部で圏論の一般論を適用してきましたが, それらを改めて確認する意味も込めて, 今回は

圏の定義
函手・自然変換
米田の補題
随伴函手
余極限と極限

を見ていきたいと思います.

圏の定義

${\mathcal{M}}$ をクラス*1とします.

${C \subset \mathcal{M} \times \mathcal{M}}$ を部分クラスとし, クラス関数 ${c : C \to \mathcal{M}}$ が与えられているものとします. ${(x, y) \in C}$ のとき ${c(x, y) = xy}$ と書き, ${xy}$ が定義されている(defined)と言います. ${(x, y) \not\in C}$ のときは ${xy}$ は定義されていない(undefined)と言います.

${\mathcal{M}}$ と ${C}$ の組が以下の公理を満たすとき, これを圏(category)であると言います. また, このとき ${\mathcal{M}}$ の要素を射(map)と言います.

公理 1. ${x, y, z \in \mathcal{M}}$ において以下が同値である.

${xy}$ と ${yz}$ が定義されている.
${(xy)z}$ が定義されている.
${x(yz)}$ が定義されている.
${(xy)z}$ と ${x(yz)}$ が定義されていて常に等しい( ${(xy)z = x(yz)}$ ).

公理 2. 以下を満たす ${e \in \mathcal{M}}$ を恒等射(identity map)という.

「 ${ex}$ または ${xe}$ の少なくとも一方が定義されるならば, その定義されているものは常に ${x}$ に等しい.」

いかなる ${x \in \mathcal{M}}$ に対しても, ${e_L x = x = x e_R}$ を満たす恒等射 ${e_L, e_R}$ が存在する.

命題 0.1. ${e, e'}$ が恒等射で ${ex}$ と ${e'x}$ がともに定義されているならば ${e = e'.}$

(証明) ${e(e'x) = ex = x}$ となるから, 公理 1 により ${ee'}$ は定義され, ${e = ee' = e'}$ である. ■*2

命題 0.1 と公理 2 は, 以下の性質を満たすクラス関数 ${R : \mathcal{M} \to \mathcal{M}}$ が存在することを示唆します.

${R(x)}$ は恒等射である.
${R(x)x}$ が定義されている.
${e}$ を ${ex}$ が定義されている恒等射とすれば ${e = R(x).}$

同様に, 以下の性質を満たすクラス関数 ${D : \mathcal{M} \to \mathcal{M}}$ も存在します.

${D(x)}$ は恒等射である.
${xD(x)}$ が定義されている.
${e}$ を ${xe}$ が定義されている恒等射とすれば ${e = D(x).}$

命題 0.2. ${D(x) = R(y)}$ ならば, かつその時に限り ${xy}$ が定義される.

(証明) only if について. ${xy = (xD(x))y}$ であるから, 公理 1 により ${D(x)y}$ が定義される. 一方 ${R(y)y}$ も定義されており, ${D(x)}$ も ${R(y)}$ も恒等射であるから ${D(x) = R(y).}$
if について. ${D(x) = R(y) = e}$ とおくと ${xe}$ と ${ey}$ がともに定義されているので, 公理 1 により ${xy = (xe)y = x(ey)}$ も定義される. ■

命題 0.3. ${xy}$ が定義されるならば ${D(xy) = D(y), R(xy) = R(x).}$

(証明) ${xy}$ と ${yD(y)}$ がともに定義されているので, 公理 1 により ${(xy)D(y)}$ が定義されており ${D(xy) = D(y)}$ である. ${R(xy) = R(x)}$ も同様に示される. ■

ここで, クラス ${\mathcal{O}}$ を, その要素が ${\mathcal{M}}$ の恒等射と 1 対 1 に対応するようなものとします. ${\mathcal{O}}$ の要素は対象(object)と呼ばれ, ${A \in \mathcal{O}}$ に対応する ${\mathcal{M}}$ の要素を ${1_A}$ で表すことにします.

${x \in \mathcal{M}}$ に対して ${B \in \mathcal{O}}$ が ${x}$ の値域(range)であるとは, ${1_B = R(x)}$ であることと定義します. また, ${A \in \mathcal{O}}$ が ${x}$ の定義域(domain)であるとは, ${1_A = D(x)}$ であることと定義します.

命題 0.2 と 0.3 は, 集合間の写像に対して期待される性質を圏論の言葉に翻訳しています.

今後は, 圏 ${\mathcal{C}}$ とは, 上記の性質を満たしているようなクラス ${\mathcal{O}}$ と ${\mathcal{M}}$ の組 ${\mathcal{C} = (\mathcal{O}, \mathcal{M})}$ であると考えることにします. とりわけ, 圏 ${\mathcal{C}}$ の対象, ないし射であることを強調するときは ${\mathcal{O}_\mathcal{C}, \mathcal{M}_\mathcal{C}}$ と表記することにします.

${A, B \in \mathcal{O}}$ に対して, ${\mathcal{C}(A, B) \subset \mathcal{M}}$ を, 定義域が ${A}$ かつ値域が ${B}$ であるような射 ${x \in \mathcal{M}}$ の全体からなるクラスとします. ${x \in \mathcal{C}(A, B)}$ であるとき, ${x : A \to B}$ と表記します. しばしば ${A \overset{x}{\longrightarrow} B}$ と表記したり, また射 ${x}$ の表記を省略して単に $A \to B$ と表記することもあります.

${A \to B}$ と ${B \to C}$ の合成を ${A \to B \to C}$ と表記します. ${A \to B \to C = A \to D \to C}$ の代わりの表記として, 以下の可換図式を用います.

${\require{AMScd}\begin{CD} A @>>> B \\ @VVV @VVV \\ D @>>> C \end{CD}}$

*1:公理的集合論で言うところの「クラス」です. 定式化については Bernays-Gödel の公理系を使うのが一般的だと思われます.

*2:以下, 証明終了の記号として使います.

2016-05-09

Catalan 数の計算について

数学・代数

Catalan 数のことは語らんよ ? …嘘です, ちょっとだけ語らせて !

先だって発売された新刊「数学ガールの秘密ノート/場合の数」に Catalan 数が登場する.

数学ガールの秘密ノート/場合の数 (数学ガールの秘密ノートシリーズ)

作者: 結城浩
出版社/メーカー: SBクリエイティブ
発売日: 2016/04/20
メディア: 単行本
この商品を含むブログ (2件) を見る

$\mathrm{C}_n = {2n \choose n} - {2n \choose n + 1} = \frac{1}{n + 1} {2n \choose n}.$

同書では, 二項係数を一度階乗を使って書き直して計算していたが, ${2n \choose n}$ は最終的にそのままの形で残るので, 以下のように計算することもできる.

${\begin{align} {2n \choose n} - {2n \choose n + 1} &= {2n \choose n} - {2n \choose n - 1} \\ &= {2n \choose n} - \frac{n}{2n + 1} {2n + 1 \choose n} \\ &= {2n \choose n} - \frac{n}{2n + 1} {2n + 1 \choose n + 1} \\ &= {2n \choose n} - \frac{n}{2n + 1} \frac{2n + 1}{n + 1} {2n \choose n} \\ &= {2n \choose n} - \frac{n}{n + 1} {2n \choose n} \\ &= \frac{1}{n + 1} {2n \choose n}. \end{align}}$

2016-04-21

直観主義論理の入り口～Heyting 代数～(その 10・最終回)

数学・基礎論

完備 Heyting 代数

Heyting 代数は束として完備であるとき, 完備 Heyting 代数(complete Heyting algebra)と言います. 良く cHa などと略されます.

同様に Boole 代数が束として完備であるとき, 完備 Boole 代数(complete Boole algebra, cBa)と言います.

既に見たように, Boole 代数は Heyting 代数なので, cBa は cHa になっていますが, 実は無限分配律
$(\bigvee X) \wedge a = \bigvee (X \wedge a)$
を満たす完備束 $L$ は cHa となることが以下のように示されます. ただし $X \subset L, a \in L$ に対して
$X \wedge a = \{ x \wedge a | x \in X\}$
と定義します.

$P(a,b) = \{ x | x \wedge a \le b \}$ と置くとき, 完備性により $\bigvee P(a,b)$ が存在します. このとき無限分配律が成り立つことにより
$( \bigvee P(a,b) ) \wedge a = \bigvee(P(a,b) \wedge a) \le b$
なので $\bigvee P(a,b) \in P(a,b)$ が成り立ち, したがって $\max P(a,b)$ が存在するので $L$ は cHa.

Heyting 代数はなぜ直観主義論理への入り口なのか ?

今回, 「直観主義論理への入り口」と題して Heyting 代数を紹介してきましたが, なぜ Heyting 代数は直観主義論理への入り口なのでしょうか ?

既に見たように, (完備) Boole 代数では $\neg \neg x = x$ や $x \vee \neg x = 1$ と言った見慣れた式が成り立ちますが, (完備) Heyting 代数ではこれらの式は一般には成り立ちません.

古典論理は真偽値の集合を完備 Boole 代数に取ったものと考えられますが, もし, 真偽値の集合を完備 Heyting 代数に取ったらどうなるでしょうか ? そのような論理体系では, もはや排中律は成り立ちません.

これは一見すると少し変わった論理体系のように思えます. しかし, もう少し「人間的な」見方をすると, ある事柄 $P$ について, $P$ であることを確認する方法がなかったからと言って $P$ ではないと言い切るのは自然でしょうか ?

このように, 実は排中律が成り立たない論理体系の方が実は人間の感覚により近いのです. そして, それを数学の言葉で実現するための入り口が Heyting 代数なのです.

完備 Heyting 代数は層の理論の定式化にも用いられ, 必然的に層と直観主義論理は密接な関係にあります.

このあたりの話を知りたい方には, 以下の書籍をお勧めします.

層・圏・トポス―現代的集合像を求めて

作者: 竹内外史
出版社/メーカー: 日本評論社
発売日: 1978/01/20
メディア: 単行本
購入: 3人クリック: 39回
この商品を含むブログ (17件) を見る

OD>直観主義的集合論 (紀伊國屋数学叢書 20)

作者: 竹内外史
出版社/メーカー: 紀伊國屋書店
発売日: 2008/11
メディア: 単行本
クリック: 3回
この商品を含むブログを見る

これらの書籍で用いられる圏の理論により詳しい書籍としては

Categories for the Working Mathematician (Graduate Texts in Mathematics)

作者: Saunders Mac Lane
出版社/メーカー: Springer
発売日: 2013/10/04
メディア: ペーパーバック
クリック: 4回
この商品を含むブログを見る

和訳本もあります.

圏論の基礎

作者: S.マックレーン,Saunders MacLane,三好博之,高木理
出版社/メーカー: 丸善出版
発売日: 2012/07/17
メディア: 単行本
クリック: 25回
この商品を含むブログ (4件) を見る

層の理論と論理学の関係については

Sheaves in Geometry and Logic: A First Introduction to Topos Theory (Universitext)

作者: Saunders MacLane,Ieke Moerdijk
出版社/メーカー: Springer
発売日: 1994/11/01
メディア: ペーパーバック
クリック: 6回
この商品を含むブログ (3件) を見る

補遺 : 古い束論の洋書などを参照する場合, Heyting 代数は "Brouwer lattices" という名称で紹介されています.

2016-04-20

直観主義論理の入り口～Heyting 代数～(その 9)

数学・基礎論

前回に引き続き Heyting 代数の性質を見ていきます.

最小元 $0$ を持つ Heyting 代数 $H$ において $\neg x = x \to 0$ と定義し, これを $x$ の擬補元と言うのでした. 今回は擬補元の性質を中心に見ていきます.

1. $x \le y$ ならば $\neg y \le \neg x.$
$\neg y = y \to 0 \le x \to 0 = \neg x.$

2. $x \wedge \neg x = 0.$
$\neg x$ の定義より明らか.

3. $x \le \neg \neg x$
2. より $x \le \neg x \to 0 = \neg \neg x.$

4. $\neg x = \neg \neg \neg x.$
3. で $x$ を $\neg x$ で置き換えると $\neg x \le \neg \neg \neg x,$ 一方で 3. に 1. を適用すると $\neg \neg \neg x \le \neg x,$ よって $\neg x = \neg \neg \neg x.$

5. $\neg(x \vee y) = \neg x \wedge \neg y.$
${\begin{align} \neg(x \vee y) &= (x \vee y) \to 0 \\ &= (x \to 0) \wedge (y \to 0) \\ &= \neg x \wedge \neg y. \end{align}}$

6. $\neg(x \wedge y) = \neg \neg(\neg x \vee \neg y).$
これは長いので証明は省略.
4., 5. と前記事の 7. を使えば証明可能.

正則性

さて, $x \le \neg \neg x$ は常に成り立つのですが, 等号 $x = \neg \neg x$ に関しては常に成り立つとは限りません. $x \in H$ については, 以下の 2 条件が同値であることが分かります.

$x = \neg \neg x.$
$x = \neg y$ となる $y \in H$ が存在する.

$1. \Rightarrow 2.$ は明らかですが, $2. \Rightarrow 1.$ については
$x = \neg y \Rightarrow \neg \neg x = \neg \neg \neg y = \neg y = x.$

$x \in H$ が上のいずれかの条件(したがって両方)を満たすとき, $x$ は正則(regular)であると言います. もし全ての $x \in H$ が正則ならば, $H$ は Boole 代数であることが, 以下のように示されます.

$y = \neg(x \vee \neg x)$ と置きます. 定義により $y \wedge (x \vee \neg x) = 0$ です. 分配則により
$0 = y \wedge (x \vee \neg x) = (y \wedge x) \vee (y \wedge \neg x)$
なので $y \wedge x = 0$ と $y \wedge \neg x = 0$ がともに成り立ちます. 故に $y \le x \to 0 = \neg x$ かつ $y \le \neg x \to 0 = \neg \neg x = x$ が成り立つので $y \le \neg x \wedge x = 0,$ すなわち $y = 0.$
よって $x \vee \neg x = \neg \neg(x \vee \neg x) = \neg y = \neg 0 = 1.$
以上により $\neg x$ は $x$ の補元となり, $H$ は Boole 代数である.