2016-06-30

楽しい圏論(その 7)

ある実例

${R}$ を可換環とします. 集合 ${X}$ が与えられたとき, ${X}$ の元を基底とする自由 ${R}$ -加群が作れます. これを ${FX}$ で表すことにします. すると函手 ${F : \mathbf{Set} \to R\text{-}\mathbf{Mod}}$ が作れます.

一方, ${R}$ -加群 ${M}$ に対して, ${R}$ -加群であることを忘れてただの集合とみなす函手*1 ${U : R\text{-}\mathbf{Mod} \to \mathbf{Set}}$ が作れます. 射も ${R}$ -準同型であることを忘れて単に集合間の写像とみなします.

このとき, 以下の関係が成り立ちます.
${\theta_{X, M} : \hom(FX, M) \ni h \stackrel{\cong}{\longmapsto} h|_X \in \hom(X, UM)}$
つまり, ${X}$ を基底の集合とする自由 ${R}$ -加群から任意の ${R}$ -加群への ${R}$ -準同型は, 基底の像によって完全に決定されるということです.

さらに, 以下のような自然性が成り立ちます. 第一に, 写像 ${f : X \to Y}$ があるとき, ${h \in \hom(FY, M)}$ に対して
${\begin{align} (\hom(f, UM) \circ \theta_{Y, M})(h) &= \hom(f, UM)(h_Y) \\ &= h_Y \circ f, \\ (\theta_{X, M} \circ \hom(Ff, M))(h) &= \theta_{X, M}(h \circ Ff) \\ &= (h \circ Ff)_X \\ &= h_Y \circ f. \end{align}}$
${\require{AMScd}\begin{CD} \hom(FY, M) @>{\hom(Ff, M)}>> \hom(FX, M) \\ @V{\theta_{Y, M}}VV \circlearrowleft @VV{\theta_{X, M}}V \\ \hom(Y, UM) @>>{\hom(f, UM)}> \hom(X, UM). \end{CD}}$

第二に, ${R}$ -準同型 ${g : M \to N}$ があるとき, ${h' \in \hom(FX, M)}$ に対して
${\begin{align} (\hom(X, Ug) \circ \theta_{X, M})(h') &= \hom(X, Ug)(h'_X) \\ &= Ug \circ h'_X \\ &= (g \circ h')_X, \\ (\theta_{X, N} \circ \hom(FX, g))(h') &= \theta_{X, N}(g \circ h') \\ &= (g \circ h')_X. \end{align}}$
${\require{AMScd}\begin{CD} \hom(FX, M) @>{\hom(FX, g)}>> \hom(FX, N) \\ @V{\theta_{X, M}}VV \circlearrowleft @VV{\theta_{X, N}}V \\ \hom(X, UM) @>>{\hom(X, Ug)}> \hom(X, UN). \end{CD}}$

今回からしばらくの間, このような現象を一般化した概念である「随伴函手」について書いていきます.

随伴函手

圏 ${C}$ と ${D}$ の間に函手 ${F : D \to C}$ と ${U : C \to D}$ があって, ${c}$ と ${d}$ において自然な同型
${C(Fd, c) \cong D(d, Uc)}$
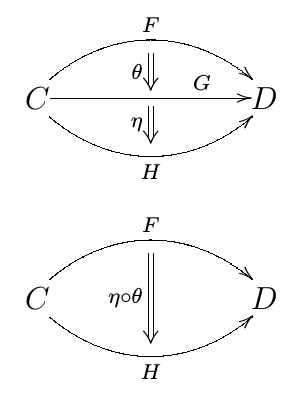
が存在するとき, ${F}$ は ${U}$ の左随伴函手(left adjoint functor)であると言います. また, このとき同時に, ${U}$ は ${F}$ の右随伴函手(right adjoint functor)であると言います. 記号では ${F \dashv U}$ と書いている書籍もあります. 図にすると以下のようになります.

函手 ${U : C \to D}$ に対して函手 ${F : D \to C}$ で ${U}$ の左随伴函手であるようなものが存在するとき, ${U}$ は左随伴函手を持つ, という表現をします. 右随伴函手を持つ, という表現も同様です.

定義において双対を取ると ${C(c, F^\mathrm{op}d) \cong D(U^\mathrm{op}c, d)}$ なので, ${U}$ が左随伴函手を持つことと ${U^\mathrm{op}}$ が右随伴函手を持つこととは同値です. この意味で, 左随伴函手と右随伴函手は互いに双対の概念になっています.

*1:忘却函手(forgetful functor)と言います.

2016-06-26

楽しい圏論(その 6)

数学・基礎論

今回はいよいよ米田の補題を証明しますが, 少しだけ準備をします.

双対圏(再)

以前, 圏 ${C}$ の双対圏 ${C^\mathrm{op}}$ を定義しましたが, 圏 ${C}$ における言明 ${\mathrm{\Sigma}}$ は, 双対圏に写ることによって双対言明 ${\mathrm{\Sigma}^*}$ に書き換えられます. ${(C^{\mathrm{op}})^{\mathrm{op}} = C}$ であることを考えれば, 圏 ${C^{\mathrm{op}}}$ における言明 ${\mathrm{\Sigma}}$ が ${C}$ においては双対言明 ${\mathrm{\Sigma}^*}$ に書き換えられることになります.

以前, 束論の話の中で束 ${L}$ は圏とみなせる, という話をしましたが, ${L}$ が束ならば ${L^{\mathrm{op}}}$ も束なので, 一般の束においてある命題が成り立てば, 常にその双対命題も成り立つ, ということが圏論からもわかる, という理屈になります.

なお, 函手 ${F : C \to D}$ があるとき, ${F^{\mathrm{op}}(c) = Fc, F^{\mathrm{op}}(f^{\mathrm{op}}) = (Ff)^{\mathrm{op}}}$ とすれば函手 ${F^{\mathrm{op}} : C^{\mathrm{op}} \to D^{\mathrm{op}}}$ が得られます.

米田の補題の証明

ステートメントは前回紹介しましたが, ここでは上記の双対圏の話を踏まえて以下の形で証明します.

米田の補題 ${C}$ は局所的に小さな圏とする.
${F : C \to \mathbf{Set}}$ を函手とするとき自然同型
${y : \mathrm{Nat}(Yc, F) \cong Fc}$
が存在する. ただし ${Y : C^{\mathrm{op}} \to \mathbf{Set}^C}$ は米田函手
${Yc = C(c, -) : C \to \mathbf{Set}.}$

以下, 証明です.

2016-06-25

楽しい圏論(その 5)

数学・基礎論

これまで, ${\mathcal{M}(C)}$ はクラスであると仮定してきました*1が, 実際にはより大きな圏も扱うことが多いです. したがって, 今後は特に断りがなければそのような圏も扱っているものと考えてください. また, そのような圏を扱っている場合でも, 集合論でよく使う記号( ${\in}$ など)を濫用します.

局所的に小さな圏, 小さな圏

以下, 頻繁に使う用語の定義です.

${C}$ が局所的に小さな圏(locally small category) ${\stackrel{\mathrm{def}}{\iff}}$ 任意の ${a, b \in \mathcal{O}(C)}$ に対して ${C(a, b)}$ が(小さな)集合.
${C}$ が小さな圏(small category) ${\stackrel{\mathrm{def}}{\iff}}$ ${C}$ は局所的に小さな圏でかつ ${\mathcal{O}(C)}$ が(小さな)集合.

圏の積と双函手

二つの圏 ${C_1, C_2}$ があったとき, 以下のようにして新しい圏 ${C_1 \times C_2}$ が構成できます*2.

${\mathcal{O}(C_1 \times C_2) = \{\langle a_1, a_2 \rangle | a_i \in \mathcal{O}(C_i)\},}$
${f_i \in C_i(a_i, b_i)}$ のとき ${\langle f_1, f_2 \rangle : \langle a_1, a_2 \rangle \to \langle b_1, b_2 \rangle,}$
${\langle g_1, g_2 \rangle \langle f_1, f_2 \rangle = \langle g_1 f_1, g_2 f_2 \rangle.}$

特殊な函手 ${P_i : C_1 \times C_2 \to C_i}$ を以下のように定義します.

${a_i \in \mathcal{O}(C_i), f_i : a_i \to b_i}$ に対して ${P_i\langle a_1, a_2 \rangle = a_i, P_i\langle f_1, f_2 \rangle = f_i.}$

この圏の積は, 以下のような普遍性を持ちます.

函手 ${F_i : D \to C_i}$ があったとき, 函手 ${G : D \to C_1 \times C_2}$ で ${P_i G = F_i}$ を満たすものが存在します. 実際 ${Gd = \langle F_1 d, F_2 d \rangle \ (d \in \mathcal{O}(D)), Gh = \langle F_1 h, F_2 h \rangle \ (h \in \mathcal{M}(D))}$ と置けばよいでしょう.

さて, 函手 ${F : C_1 \times C_2 \to D}$ を特に双函手(bifunctor)と言います. 特に重要なのは, 局所的に小さな圏 ${C}$ に対する hom 函手
${C(-, -) : C^{\mathrm{op}} \times C \to \mathbf{Set}}$
でしょう*3. ${f : a_1 \gets a_2, g : b_1 \to b_2}$ に対して
${C(f, g) : C(a_1, b_1) \ni h \mapsto ghf \in C(a_2, b_2)}$
とすれば, これが実際に函手になっていることを見るのは容易でしょう.

さて, この hom 函手においてある ${c \in \mathcal{O}(C)}$ を固定することで, 函手
${Y_C(c) = C(-, c) : C^{\mathrm{op}} \to \mathbf{Set}}$
が得られます. つまり ${Y_C}$ は ${C}$ から ${\mathbf{Set}^{C^{\mathrm{op}}}}$ への函手を与えていることになります. これを米田函手(Yoneda functor)と言います. 同様に
${Y^C(c) = C(c, -) : C \to \mathbf{Set}}$
から得られる函手 ${Y^C : C^{\mathrm{op}} \to \mathbf{Set}^C}$
もやはり米田函手と言います.

充満函手, 忠実函手

${F : C \to D}$ を函手とするとき, ${F}$ は函数 ${C(a, b) \to D(Fa, Fb)}$ を導きます. 以下の用語を定義します.

${F}$ が充満(full) ${\stackrel{\mathrm{def}}{\iff}}$ 任意の ${g \in D(Fa, Fb)}$ に対して ${g = Ff}$ となる ${f \in C(a, b)}$ が存在する.
${F}$ が忠実(faithful) ${\stackrel{\mathrm{def}}{\iff}}$ ${f_1, f_2 \in C(a, b)}$ に対して ${Ff_1 = Ff_2}$ ならば ${f_1 = f_2.}$

米田の補題

証明は次回行います. 二つの函手 ${F, G : C \to D}$ に対して, ${F}$ から ${G}$ への自然変換の全体 ${D^C(F, G)}$ を ${\mathrm{Nat}(F, G)}$ と書くことにします.

米田の補題 ${C}$ を局所的に小さな圏とする.
${F : C^{\mathrm{op}} \to \mathbf{Set}}$ を函手とするとき自然同型
${\mathrm{Nat}(Y_C(c), F) \cong Fc }$
が存在する. 特に ${F = Y_C(c') = C(-, c')}$ に取れば
${\mathrm{Nat}(C(-, c), C(-, c')) = \mathrm{Nat}(Y_C(c), Y_C(c')) \cong Y_C(c')(c) = C(c, c'),}$
すなわち米田函手は充満かつ忠実である.

特に米田の補題の後半は良く使います. すなわち任意の ${x \in \mathcal{O}(C)}$ について自然同型 ${C(x, c) \cong C(x, c')}$ が存在すれば, 対象として ${c \cong c'}$ が成り立つということです.

ここに, 二つの対象 ${c, c' \in \mathcal{O}(C)}$ が同型(isomorphic)であるとは, 二つの射 ${f : c \to c', g : c' \to c}$ が存在して ${gf = 1_c, fg = 1_{c'}}$ を満たすことを言い, このような ${f}$ (や ${g}$ ) を同型射(isomorphism)と言います.

*1:その部分クラスと同一視できる ${\mathcal{O}(C)}$ ももちろんクラスになる.

*2:より普遍的な構成方法は後ほど紹介します.

*3: ${\mathbf{Set}}$ は全ての小さな集合と写像の圏です.

2016-06-25

楽しい圏論(その 4)

数学・基礎論

今後, ${F(a), F(f)}$ などは単に ${Fa, Ff}$ と書きます. また, 射や函手の合成記号は省いて ${gf, GF}$ などと書きます.

自然変換の垂直合成と函手圏

圏 ${C}$ から圏 ${D}$ への函手 ${F, G, H : C \to D}$ と自然変換 ${\theta : F \Rightarrow G, \eta : G \Rightarrow H}$ が与えられたとき, 垂直合成(vertical composition) ${\eta \circ \theta}$ を ${(\eta \circ \theta)_a := \eta_a \theta_a \ (a \in \mathcal{O}(C))}$ で定義します.

これが ${F}$ から ${H}$ への自然変換になっていることは, 次図の可換性から明らかでしょう.

${\require{AMScd}\begin{CD} Fa @>{Ff}>> Fb \\ @V{\theta_a}VV @VV{\theta_b}V \\ Ga @>{Gf}>> Gb \\ @V{\eta_a}VV @VV{\eta_b}V \\ Ha @>>{Hf}> Hb, \end{CD}}$
${(a, b \in \mathcal{O}(C), f \in C(a,b).)}$

自然変換の垂直合成は結合法則を満たし, これによって ${C}$ から ${D}$ への函手の全体は函手を対象, 自然変換を射とする圏になります. これを函手圏(functor category)と言い, ${D^C}$ で表します.

自然変換の水平合成

自然変換にはもう一つ, 水平合成(horizontal composition)と言われる合成があります. これは次図のように圏 ${C}$ から圏 ${D}$ への函手 ${F_0, F_1 : C \to D}$ と, 圏 ${D}$ から圏 ${E}$ への函手 ${G_0, G_1 : D \to E}$ , さらに自然変換 ${\theta : F_0 \Rightarrow F_1, \eta : G_0 \Rightarrow G_1}$ があるときに定義されます.

以下, 長くなるので折りたたみ.

2016-06-19

楽しい圏論(その 3)

数学・基礎論

反変函手と双対圏

前回は函手を定義しましたが, もう一つ, 反変函手(contravariant functor)と言われるものがあります.

${e}$ が ${\mathcal{M}_1}$ の恒等射ならば ${F(e)}$ は ${\mathcal{M}_2}$ の恒等射である.
${\mathcal{M}_1}$ において ${xy}$ が定義されているならば ${\mathcal{M}_2}$ において ${F(y)F(x)}$ が定義されており, ${F(xy) = F(y)F(x)}$ である.

一つ目は通常の函手(共変函手(covariant functor)と言われることもあります)と同じですが, 二つ目が変わっていて, 反変函手の場合は射の合成の順番が入れ替わります.

反変函手は, 以下のような双対圏(dual category)の概念を導入することで, 共変函手と区別することなく扱うことができます.

${\mathcal{M}}$ を射のクラスとするとき, 双対射のクラス ${\mathcal{M}^{\mathrm{op}} = \{x^{\mathrm{op}} | x \in \mathcal{M}\}}$ において ${x^{\mathrm{op}} y^{\mathrm{op}} = (yx)^{\mathrm{op}}}$ と定めます. ${e \in \mathcal{M}}$ が恒等射ならば ${e^{\mathrm{op}} \in \mathcal{M}^{\mathrm{op}}}$ も恒等射です. ${(1_A)^{\mathrm{op}} = 1_{A^{\mathrm{op}}}}$ となるように定めることで ${\mathcal{O}^{\mathrm{op}} = \{A^{\mathrm{op}} | A \in \mathcal{O}\}}$ と表せます.

このとき

${D(x)^{\mathrm{op}}}$ は恒等射
${D(x)^{\mathrm{op}} x^{\mathrm{op}} = (xD(x))^{\mathrm{op}}}$ は定義されている

ので, ${R(x^{\mathrm{op}}) = D(x)^{\mathrm{op}}}$ です. 同様に ${D(x^{\mathrm{op}}) = R(x)^{\mathrm{op}}}$ です. よって ${A \overset{x}{\longrightarrow} B}$ は双対圏において ${B^{\mathrm{op}} \overset{x^{\mathrm{op}}}{\longrightarrow} A^{\mathrm{op}}}$ に変換されます.

${A \in \mathcal{O}}$ と ${A^{\mathrm{op}} \in \mathcal{O}^{\mathrm{op}}}$ を同一視することによって, 双対圏とは射の向きを逆にしたもの, と考えることができます.

双対圏を使うと反変函手 ${F : \mathcal{M}_1 \to \mathcal{M}_2}$ は共変函手 ${F : {\mathcal{M}_1}^{\mathrm{op}} \to \mathcal{M}_2}$ とみなせるため, 以下は反変函手もこの同一視によって単に「函手」と言うことにします.

自然変換

最後に自然変換を定義します.

二つの函手 ${F, G : \mathcal{C}_1 \to \mathcal{C}_2}$ があるとき, ${\eta : F \Rightarrow G}$ が自然変換(natural transformation)であるとは, 以下の公理を満たすことを言います.

${A \in \mathcal{O}_1}$ に対して ${\eta(A) \in \mathcal{C}_2(F(A), G(A)).}$
${x \in \mathcal{C}_1(A, B)}$ に対して次図は可換である.

${\require{AMScd}\begin{CD} F(A) @>{F(x)}>> F(B) \\ @V{\eta(A)}VV @VV{\eta(B)}V \\ G(A) @>>{G(x)}> G(B) \end{CD}}$

(標数 ${0}$ の体 ${K}$ 上の)有限次元ベクトル空間 ${V}$ について ${V^* := \hom(V, K)}$ とするとき, 「自然な」同型 ${V \cong V^{**}}$ があるのですが, この自然な, という意味は以下の通りです.

${\theta_V : V \to V^{**}}$ を ${\theta_V(x)(\varphi) = \varphi(x) \ (x \in V, \varphi \in V^*)}$ で定めるとき, 任意の線形写像 ${f : V \to W}$ に対して ${f^{**} \circ \theta_V = \theta_W \circ f}$ が成り立ちます. ただし ${f^* : W^* \ni \psi \mapsto \psi \circ f \in V^*.}$ 実際, 任意の ${x \in V}$ と ${\psi \in W^*}$ に対して

${\begin{align} (f^{**} \circ \theta_V)(x)(\psi) &= (\theta_V(x) \circ f^*)(\psi) \\ &= \theta_V(x)(\psi \circ f) \\ &= \psi(f(x)), \end{align}}$
${\begin{align} (\theta_W \circ f)(x)(\psi) &= \theta_W(f(x))(\psi) \\ &= \psi(f(x)). \end{align}}$

従って次図は可換になります.

${\require{AMScd}\begin{CD} V @>{f}>> W \\ @V{\theta_V}VV @VV{\theta_W}V \\ V^{**} @>>{f^{**}}> W^{**} \end{CD}}$

以上の証明には ${V}$ が有限次元であることは使っていませんが, ${V}$ が有限次元ならば ${\theta_V : V \to V^{**}}$ は同型写像になります.

元々は, このような現象を一般化する概念として自然変換を定義するべく, 函手や圏の概念ができていったようです.

記法の約束事

今後の記法に関する約束事です.

圏 : アルファベット大文字 ${C, D, \dots}$
対象 : アルファベット小文字 ${a, b, \dots}$ , 圏 ${C}$ の対象の全体は ${\mathcal{O}(C)}$ で表す.
射 : アルファベット小文字 ${f, g, h, \dots}$ , 圏 ${C}$ の対象 ${a}$ から ${b}$ への射の全体は ${C(a, b)}$ で表す.
函手 : アルファベット大文字 ${F, G, H, \dots}$
自然変換 : ギリシャ小文字 ${\theta, \eta, \dots}$

2016-06-16

楽しい圏論(その 2)

数学・基礎論

一ヶ月ほど間が空いてしまいましたが, ようやくブログを書ける状態になってきたので再開します.

函手の定義

${\mathcal{M}_1, \mathcal{M}_2}$ を二つの圏(の射のクラス)とします. クラス関数 ${F : \mathcal{M}_1 \to \mathcal{M}_2}$ は, 以下の二つの公理を満たすとき, 函手(functor)であると言います.

${e}$ が ${\mathcal{M}_1}$ の恒等射ならば ${F(e)}$ は ${\mathcal{M}_2}$ の恒等射である.
${\mathcal{M}_1}$ において ${xy}$ が定義されているならば ${\mathcal{M}_2}$ において ${F(x)F(y)}$ が定義されており, ${F(xy) = F(x)F(y)}$ である.

${\mathcal{O}_1, \mathcal{O}_2}$ をそれぞれ ${\mathcal{M}_1, \mathcal{M}_2}$ に対応する対象のクラスとするとき, ${A \in \mathcal{O}_1}$ に対して ${F(A) \in \mathcal{O}_2}$ を
${1_{F(A)} = F(1_A)}$
なる対象と定めることにより, ${F}$ はクラス関数 ${F : \mathcal{O}_1 \to \mathcal{O}_2}$ を導きます.

前回, 射の値域と定義域の話をしました. ${1_B = R(x)}$ を満たす ${B}$ のことを ${Range(x)}$ と, また ${1_A = D(x)}$ を満たす ${A}$ のことを ${Domain(x)}$ と書くことにします.

命題 0.4. ${F(Domain(x)) = Domain(F(x)), F(Range(x)) = Range(F(x)).}$

(証明)*1

${F(D(x))}$ は恒等射で, かつ ${F(x)F(D(x)) = F(xD(x))}$ が定義されているから ${F(D(x)) = D(F(x)).}$ 同様に ${F(R(x)) = R(F(x)).}$ 以上から従う. ■

タネ本

何だか射の話ばかりが出てきて, 多分他の書籍で圏論を知った人は驚くかも知れませんが, これでちゃんと理論になっています. この方法にはタネ本があります.

Abelian Categories

作者: Peter Freyd
出版社/メーカー: Joanna Cotler Books
発売日: 1966/12
メディア: ハードカバー
この商品を含むブログを見る

(自分が持っているものとは出版社が違いますが, 中身は多分同じ ?)

この本では, 今回のようなやり方で圏と函手を定義しています.

特殊な圏

以下, 頻繁に(?)使用する特殊な圏をいくつか定義します.

射のクラスが空集合である圏を空圏と言い, ${\boldsymbol{0}}$ で表します. もちろん, 空圏には対象も存在しません.

射のクラスがただ一つの恒等射だけからなる圏を ${\boldsymbol{1}}$ で表します. ${\boldsymbol{1} = (\{*\}, \{1_*\}).}$

射のクラスが二つの恒等射 ${1_A, 1_B}$ と, 恒等射ではないただ一つの射 ${x \ (D(x) = 1_A, R(x) = 1_B)}$ の三つの元からなる集合である圏を ${\boldsymbol{2}}$ で表します. これは後で述べるように, 集合 ${\{0, 1\}}$ に通常の大小関係で定まる順序を入れた順序集合を圏とみなしたものと同じです.

射のクラスが

三つの恒等射 ${1_A, 1_B, 1_C}$
恒等射でない二つの射 ${x, y \ (D(y) = 1_A, R(y) = D(x) = 1_B, R(x) = 1_C)}$ とその合成 ${xy}$

の 6 個の元からなる集合である圏を ${\boldsymbol{3}}$ で表します. これも後で述べるように, 集合 ${\{0, 1, 2\}}$ に通常の大小関係で定まる順序を入れた順序集合を圏とみなしたものと同じです.

射のクラスが, 二つの恒等射 ${1_A, 1_B}$ と恒等射でない二つの射 ${x, y}$ からなり, ${D(x) = D(y) = 1_A}$ かつ ${R(x) = R(y) = 1_B}$ であるものとします. この圏は ${\downdownarrows}$ で表します.

順序集合は圏である

${A}$ が順序集合であるとは, 台集合 ${A}$ と関係 ${O \subset A \times A}$ の組 ${(A, O)}$ が以下の条件を満たすことでした.

(反射律) ${\Delta_A \subset O,}$ ただし ${\Delta_A = \{(a, a) | a \in A\}}$ は対角集合.
(反対称律) ${O \cap O^{-1} = \Delta_A,}$ ただし ${O^{-1} = \{(b, a) | (a, b) \in O\}}$ は逆関係.
(推移律) ${O \circ O \subset O,}$ ただし ${O \circ O = \{(a, c) | (\exists b \in A)((a, b) \in O \wedge (b, c) \in O)\}}$ は関係の合成.

そこで, ${O}$ を射の集合として, 射の合成を ${(b, c) \circ (a, b) = (a, c)}$ で定めると, これを圏とみなすことができます. ${1_a = (a, a)}$ なる対応によって, ${A}$ を対象の集合とみなすことができます.

このことを使うと, 通常の数の大小関係による順序付けでもって
${\boldsymbol{2} = \{0, 1\}, \boldsymbol{3} = \{0, 1, 2\}}$
となることがわかります.

対象は函手であり, 射は函手である.

圏 ${\mathcal{C}}$ の対象は函手 ${A : \boldsymbol{1} \to \mathcal{C}}$ とみなすことができます. また ${\mathcal{C}}$ の射は函手 ${x : \boldsymbol{2} \to \mathcal{C}}$ とみなすことができます.

*1:タネ本では「特に証明することはない」と書いていますが, ざっくりと説明しておきます.

2016-05-17

楽しい圏論(その 1)

数学・基礎論

今回から, 圏論について述べていこうと思います. Heyting 代数の話の中でも, 一部で圏論の一般論を適用してきましたが, それらを改めて確認する意味も込めて, 今回は

圏の定義
函手・自然変換
米田の補題
随伴函手
余極限と極限

を見ていきたいと思います.

圏の定義

${\mathcal{M}}$ をクラス*1とします.

${C \subset \mathcal{M} \times \mathcal{M}}$ を部分クラスとし, クラス関数 ${c : C \to \mathcal{M}}$ が与えられているものとします. ${(x, y) \in C}$ のとき ${c(x, y) = xy}$ と書き, ${xy}$ が定義されている(defined)と言います. ${(x, y) \not\in C}$ のときは ${xy}$ は定義されていない(undefined)と言います.

${\mathcal{M}}$ と ${C}$ の組が以下の公理を満たすとき, これを圏(category)であると言います. また, このとき ${\mathcal{M}}$ の要素を射(map)と言います.

公理 1. ${x, y, z \in \mathcal{M}}$ において以下が同値である.

${xy}$ と ${yz}$ が定義されている.
${(xy)z}$ が定義されている.
${x(yz)}$ が定義されている.
${(xy)z}$ と ${x(yz)}$ が定義されていて常に等しい( ${(xy)z = x(yz)}$ ).

公理 2. 以下を満たす ${e \in \mathcal{M}}$ を恒等射(identity map)という.

「 ${ex}$ または ${xe}$ の少なくとも一方が定義されるならば, その定義されているものは常に ${x}$ に等しい.」

いかなる ${x \in \mathcal{M}}$ に対しても, ${e_L x = x = x e_R}$ を満たす恒等射 ${e_L, e_R}$ が存在する.

命題 0.1. ${e, e'}$ が恒等射で ${ex}$ と ${e'x}$ がともに定義されているならば ${e = e'.}$

(証明) ${e(e'x) = ex = x}$ となるから, 公理 1 により ${ee'}$ は定義され, ${e = ee' = e'}$ である. ■*2

命題 0.1 と公理 2 は, 以下の性質を満たすクラス関数 ${R : \mathcal{M} \to \mathcal{M}}$ が存在することを示唆します.

${R(x)}$ は恒等射である.
${R(x)x}$ が定義されている.
${e}$ を ${ex}$ が定義されている恒等射とすれば ${e = R(x).}$

同様に, 以下の性質を満たすクラス関数 ${D : \mathcal{M} \to \mathcal{M}}$ も存在します.

${D(x)}$ は恒等射である.
${xD(x)}$ が定義されている.
${e}$ を ${xe}$ が定義されている恒等射とすれば ${e = D(x).}$

命題 0.2. ${D(x) = R(y)}$ ならば, かつその時に限り ${xy}$ が定義される.

(証明) only if について. ${xy = (xD(x))y}$ であるから, 公理 1 により ${D(x)y}$ が定義される. 一方 ${R(y)y}$ も定義されており, ${D(x)}$ も ${R(y)}$ も恒等射であるから ${D(x) = R(y).}$
if について. ${D(x) = R(y) = e}$ とおくと ${xe}$ と ${ey}$ がともに定義されているので, 公理 1 により ${xy = (xe)y = x(ey)}$ も定義される. ■

命題 0.3. ${xy}$ が定義されるならば ${D(xy) = D(y), R(xy) = R(x).}$

(証明) ${xy}$ と ${yD(y)}$ がともに定義されているので, 公理 1 により ${(xy)D(y)}$ が定義されており ${D(xy) = D(y)}$ である. ${R(xy) = R(x)}$ も同様に示される. ■

ここで, クラス ${\mathcal{O}}$ を, その要素が ${\mathcal{M}}$ の恒等射と 1 対 1 に対応するようなものとします. ${\mathcal{O}}$ の要素は対象(object)と呼ばれ, ${A \in \mathcal{O}}$ に対応する ${\mathcal{M}}$ の要素を ${1_A}$ で表すことにします.

${x \in \mathcal{M}}$ に対して ${B \in \mathcal{O}}$ が ${x}$ の値域(range)であるとは, ${1_B = R(x)}$ であることと定義します. また, ${A \in \mathcal{O}}$ が ${x}$ の定義域(domain)であるとは, ${1_A = D(x)}$ であることと定義します.

命題 0.2 と 0.3 は, 集合間の写像に対して期待される性質を圏論の言葉に翻訳しています.

今後は, 圏 ${\mathcal{C}}$ とは, 上記の性質を満たしているようなクラス ${\mathcal{O}}$ と ${\mathcal{M}}$ の組 ${\mathcal{C} = (\mathcal{O}, \mathcal{M})}$ であると考えることにします. とりわけ, 圏 ${\mathcal{C}}$ の対象, ないし射であることを強調するときは ${\mathcal{O}_\mathcal{C}, \mathcal{M}_\mathcal{C}}$ と表記することにします.

${A, B \in \mathcal{O}}$ に対して, ${\mathcal{C}(A, B) \subset \mathcal{M}}$ を, 定義域が ${A}$ かつ値域が ${B}$ であるような射 ${x \in \mathcal{M}}$ の全体からなるクラスとします. ${x \in \mathcal{C}(A, B)}$ であるとき, ${x : A \to B}$ と表記します. しばしば ${A \overset{x}{\longrightarrow} B}$ と表記したり, また射 ${x}$ の表記を省略して単に $A \to B$ と表記することもあります.