楽しい圏論(その 4) - Red cat の数学よもやま話・新装開店

今後, ${F(a), F(f)}$ などは単に ${Fa, Ff}$ と書きます. また, 射や函手の合成記号は省いて ${gf, GF}$ などと書きます.

自然変換の垂直合成と函手圏

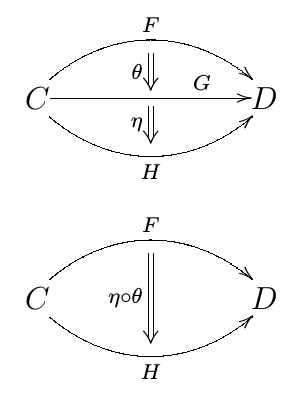
圏 ${C}$ から圏 ${D}$ への函手 ${F, G, H : C \to D}$ と自然変換 ${\theta : F \Rightarrow G, \eta : G \Rightarrow H}$ が与えられたとき, 垂直合成(vertical composition) ${\eta \circ \theta}$ を ${(\eta \circ \theta)_a := \eta_a \theta_a \ (a \in \mathcal{O}(C))}$ で定義します.

これが ${F}$ から ${H}$ への自然変換になっていることは, 次図の可換性から明らかでしょう.

${\require{AMScd}\begin{CD} Fa @>{Ff}>> Fb \\ @V{\theta_a}VV @VV{\theta_b}V \\ Ga @>{Gf}>> Gb \\ @V{\eta_a}VV @VV{\eta_b}V \\ Ha @>>{Hf}> Hb, \end{CD}}$
${(a, b \in \mathcal{O}(C), f \in C(a,b).)}$

自然変換の垂直合成は結合法則を満たし, これによって ${C}$ から ${D}$ への函手の全体は函手を対象, 自然変換を射とする圏になります. これを函手圏(functor category)と言い, ${D^C}$ で表します.

自然変換の水平合成

自然変換にはもう一つ, 水平合成(horizontal composition)と言われる合成があります. これは次図のように圏 ${C}$ から圏 ${D}$ への函手 ${F_0, F_1 : C \to D}$ と, 圏 ${D}$ から圏 ${E}$ への函手 ${G_0, G_1 : D \to E}$ , さらに自然変換 ${\theta : F_0 \Rightarrow F_1, \eta : G_0 \Rightarrow G_1}$ があるときに定義されます.

以下, 長くなるので折りたたみ.

まず, 次図のような状況を考えます.

${D}$ における可換図式
${\require{AMScd}\begin{CD} F_0 a @>{F_0 f }>> F_0 b \\ @V{\theta_a}VV @VV{\theta_b}V \\ F_1 a @>>{F_1 f }> F_1 b \end{CD}}$
をそっくり函手 ${G}$ で写すと
${\require{AMScd}\begin{CD} G F_0 a @>{G F_0 f}>> G F_0 b \\ @V{G \theta_a}VV @VV{G \theta_b}V \\ G F_1 a @>>{G F_1 f}> G F_1 b \end{CD}}$
となるので, ${(G \star \theta)_a := G \theta_a}$ と定義することで新しい自然変換 ${G \star \theta : G F_0 \Rightarrow G F_1}$ が得られます.

次に, 次図のような状況を考えます.

${C}$ の射 ${f : a \to b}$ は函手 ${F}$ によって ${Ff : Fa \to Fb}$ に写ります. このとき ${\eta : G_0 \Rightarrow G_1}$ の自然性により, 可換図式
${\require{AMScd}\begin{CD} G_0 F a @>{G_0 F f}>> G_0 F b \\ @V{\eta_{Fa}}VV @VV{\eta_{Fb}}V \\ G_1 F a @>>{G_1 F f}> G_1 F b \end{CD}}$
が成り立ちます. したがって ${(\eta \star F)_a := \eta_{Fa}}$ と定義すれば, 新しい自然変換 ${\eta \star F : G_0 F \Rightarrow G_1 F}$ が得られます.

以上の準備によって, 以下の要領で ${\theta}$ と ${\eta}$ の水平合成が得られます.

${\eta \star \theta := (G_1 \star \theta) \circ (\eta \star F_0) : G_1 F_1 \Rightarrow G_0 F_0.}$

気になるのは以下の図です.

しかし ${(G_1 \star \theta) \circ (\eta \star F_0) = (\eta \star F_1) \circ (G_0 \star \theta)}$ が成り立つことが, 以下のようにしてわかります. ${a \in \mathcal{O}(C)}$ を任意の対象とするとき, 射 ${\theta_a : F_0 a \to F_1 a}$ について ${\eta : G_0 \Rightarrow G_1}$ の自然性から可換図式
${\require{AMScd}\begin{CD} G_0 F_0 a @>{G_0 \theta_a}>> G_0 F_1 a \\ @V{\eta_{F_0 a}}VV @VV{\eta_{F_1 a}}V \\ G_1 F_0 a @>>{G_1 \theta_a}> G_1 F_1 a, \end{CD}}$
すなわち ${G_1 \theta_a \circ \eta_{F_0 a} = \eta_{F_1 a} \circ G_0 \theta_a }$ が成り立ちます.
以下, 定義により
${\begin{align} (G_1 \star \theta)_a \circ (\eta \star F_0)_a &= (\eta \star F_1)_a \circ (G_0 \star \theta)_a, \\ ( (G_1 \star \theta) \circ (\eta \star F_0) )_a &= ( (\eta \star F_1) \circ (G_0 \star \theta) )_a, \\ (G_1 \star \theta) \circ (\eta \star F_0) &= (\eta \star F_1) \circ (G_0 \star \theta). \end{align}}$

なお, 証明は略しますが, 垂直合成と水平合成に関して, 以下の図において
${(\eta_1 \circ \eta_0) \star (\theta_1 \circ \theta_0) = (\eta_1 \star \theta_1) \circ (\eta_0 \star \theta_0)}$
が成り立ちます.