トポスの定義
圏  がデカルト閉圏(cartesian closed category, CCC) であるとは, 以下の三つの函手が特定の右随伴を持つことを言います.
がデカルト閉圏(cartesian closed category, CCC) であるとは, 以下の三つの函手が特定の右随伴を持つことを言います.
これらの右随伴は
なので, CCC とは「終対象と(有限)積と冪が存在する圏」と言い換えることができます.
圏  がトポス(topos)であるとは,
がトポス(topos)であるとは,  が CCC で, かつ以下の性質を満たす部分対象分類子(subobject classifier)
が CCC で, かつ以下の性質を満たす部分対象分類子(subobject classifier)  が存在することを言います.
が存在することを言います.
任意の単射  に対して, 次図が引き戻しとなるような射
に対して, 次図が引き戻しとなるような射  が一意に存在する.
が一意に存在する.
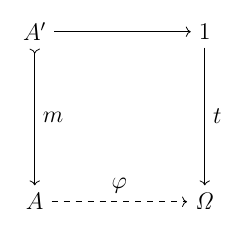
例えば  は
は  とするとトポスになります.
とするとトポスになります.