Red cat の数学よもやま話・新装開店

はてなダイアリー「Red cat の数学よもやま話」から徐々にこちらに移行していきます。

数学・代数数学・幾何

astroid に続いては cardioid の陰関数表示を.

cardioid は ${r=a(1 + \cos \theta)}$ という極方程式によって与えられる平面曲線である.

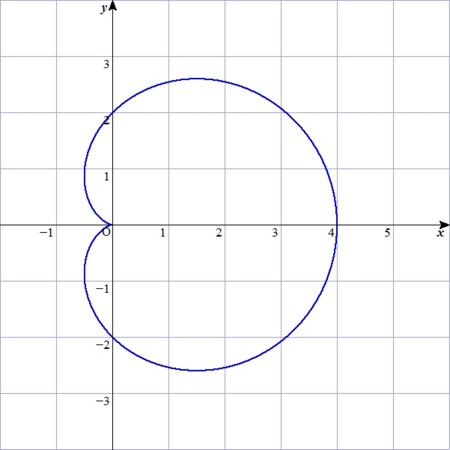
(図は ${a=2}$ )

astroid のときと同じように ${\mathbb{Q}[a, x, y, r, c, s]}$ の ideal

${\mathfrak{I}=\langle r - a(1 + c), x - rc, y - rs, r^2 - (x^2 + y^2)\rangle}$

から ${r, c, s}$ を消去すると陰関数表示が得られる.

Use QQ[a, x, y, r, c, s];
I := ideal(r - a * (1 + c), x - r * c, y - r * s, r^2 - (x^2 + y^2));
elim(r..s, I);

${- 2ax^3 + x^4 - a^2 y^2 - 2axy^2 + 2x^2 y^2 + y^4}$
なる式を得る. 整理の仕方はいろいろあるが, 一例は ${(x^2 - ax + y^2)^2 - a^2(x^2 + y^2)=0.}$